"1 violent cracking method
Find the occurrence position of mode string B in main string a, where if the length of a is n and the length of B is m, then n is m. When we match violently, we match the N-M + 1 substrings whose starting positions are 0, 1, 2,... N-M and length is m in the main string a.
Violent matching
The corresponding code is:
#include《stdio.h》
#include《string.h》
int cnt=0;
int index(char s[], char sub[])
{
int i=0;
int j=0;
while(i《strlen(s))
{
if(s[i]==sub[j])
{/ / if a single character is equal, I and j search backwards
i++;
j++;
}
else
{/ / if there is a character mismatch, I starts from the next position of the previous time, and the pattern string J starts from 0
i=i-j+1;
j=0;
}
if(j==strlen(sub))
{
cnt++;
return i-strlen(sub)+1;
}
}
return -1;
}
int main()
{
//S = "abcdabfgabefa", sub = "Abe", return 5.
char s[20],sub[10];
gets(s);
gets(sub);
printf(“%d
”,cnt);
printf(“%d
”,index(s,sub));
return 0;
}
If the main string is BBB... BBB and the mode string is bbbbc, each string should be compared m times, a total of (n-m + 1) * m times. Large time complexity = O (n * m). This method can be used for simple matching.
2 Rabin Karp algorithm
Algorithm idea: calculate the hash value of the N-M + 1 substring of the main string respectively, and then compare it with the hash value of the template string. If it is the same, then compare whether the strings are the same one by one.
Rabin Karp algorithm
However, the hash value calculation of intermediate data can be optimized. We take a simple string matching as an example to map A-Z to 0 ~ 25. Then, calculate the hash value of a string according to hexadecimal 26, for example:
Hash calculation
However, you will find that there is overlap between two adjacent substring data. For example, DAB overlaps ABC. In this way, the hash value of the next hash data can be derived from the value of the next previous data:
Optimize hash calculation
The time complexity of RK algorithm consists of two parts. The first part is to traverse all substrings to calculate hash values, and the time complexity is O (n). The second part is to compare hash values. The time complexity of this part is also o (n).
The core of this algorithm is to minimize the comparison of different data when the hash values are equal, so the hash algorithm should be as good as possible. If you feel that it is easy to collide with the letter ABC corresponding to 123, it is OK to match with prime numbers. Anyway, the purpose is the same. You can think that this is a clever way to deal with the string matching problem.
3 Boyer Moore algorithm.
Boyer Moore algorithm is a very efficient string matching algorithm. Its performance is 3 to 4 times that of the famous KMP algorithm. It is not easy to understand, but it is the most used string matching algorithm in engineering. In the past, when we matched strings, we moved from front to back to compare them one by one. The core idea of BM algorithm is to slide the pattern string back a few more bits to reduce unnecessary character comparison when a character in the pattern string cannot match the main string.
Mobile comparison
Overall, BM algorithm is quite complex. Compared with the first two, it mainly includes bad character rules and good suffix rules.
3.1 bad character rules
Bad character rule means matching from back to front according to the pattern string. When we find that a character cannot be matched. We call the characters in the main string that do not match as bad characters.
Bad character
After finding the bad character c, continue to search in the pattern string. If it is found that C cannot match any character of the pattern string, you can directly move the pattern string back by 3 bits. Continue to compare from the end of the pattern string.
Move 2 spaces
At this time, it is found that the bad character is g, but there is a G in the mode string. You can't move back 3, and the moving position is 2. Continue matching. What are the rules?
In case of transmission mismatch, the subscript position Si of the pattern string character corresponding to the bad character. If the bad character exists in the pattern string, take the first bad character from the back to the front and mark it as Xi (the first one is afraid of moving too large). If the bad character does not exist in the pattern string, xi = - 1. At this time, the mode string moves backward by digits = Si - Xi.
Bad character movement rule
If the extreme main string = cccdccccd and mode string = CCCC, the time complexity is O (n / M).
Optimal solution
But don't be happy too soon! The following situation may cause the mode string to move forward instead of backward!
Move forward?
Therefore, the BM algorithm also needs to use good suffix rules.
3.2 bad character code
In order to avoid traversing and searching from the pattern string with characters every time, a hash table is used to save each character and its subscript in the pattern string, which is convenient for rapid search.
Next, for the hash table rule, for example, a character is a byte. The occurrence position of each character in the mode string is recorded with an array of 256. The array stores the occurrence position of the mode string. The table below the array is the ASCII value corresponding to the character.
Hash rule bad character rule:
//Global variable size
private static final int SIZE = 256;
//B = pattern string array, M is the length of pattern string array, SL is hash table, default - 1
private void generateBC(char[] b, int m, int[] sl) {
for (int i = 0; i 《 SIZE; i++) {
sl[i] = -1; // Initialize sl
}
for (int i = 0; i 《 m; ++ i) {
int ascii = (int)b[i];
sl[ascii] = i;
}
}
Next, regardless of the negative number of good suffix rules and bad characters, roughly write the BM algorithm code first.
Bad character BM
public int bm(char[] a, int n, char[] b, int m) {
//Records the last position of each character in the pattern string
int[] sl = new int[SIZE];
//Build bad character hash table
generateBC(b, m, sl);
//I represents the first character of the main string aligned with the mode string
int i = 0;
while (i 《= n - m) {
int j;
for (j = m - 1; j 》= 0; j--) {
if (a[i+j] != b[j]) break;
}
if (j 《 0) {
//If the matching is successful, the position of the first matching character between the main string and the pattern string is returned
return i;
}
//Slide the mode string back to the j-BC [(int) a [i + J]] bit
i = i + (j - sl[(int)a[i+j]]);
}
return -1;
}
3.3 good suffix rules
Good suffixes are similar to bad suffixes. They match from back to front until they encounter the mismatched character X. those before the main string X are called good suffixes.
Good suffix definition
The moving rules are as follows:
If the good suffix is found in the pattern string, frame it with an X, and then align the X frame with the good suffix to continue matching.
Move rule found
When it cannot be found, if the direct moving length is m bits of the mode string, it is very likely to be excessive! The reason for excessive movement is that, for example, if you find a good suffix u, u is not found in the pattern string as a whole, but the substring D of u can match the pattern string.
Excessive movement
Therefore, at this time, we should also pay attention to whether the suffix substring of the suffix matches the prefix substring in the pattern string. Find the longest suffix substring that can match the prefix substring of the pattern string from the post suffix substring of the good suffix string, and then slide it together, such as d above.
Then calculate the backward sliding digits of bad characters and the backward sliding digits of good suffixes respectively. At this time, take their large as the backward sliding digits of mode string. In this case, the negative number of bad characters can also be avoided.
3.4 good suffix code
The core of a good suffix lies in two points:
In the pattern string, find another substring that matches the good suffix.
In the suffix substring with good suffix, find the longest suffix substring that can match the prefix substring of pattern string.
3.4.1 pretreatment
The above two core points can be solved by violence at the code level, but it is too time-consuming! We can pre calculate the position of each suffix substring of the pattern string and the corresponding matching substring by preprocessing the pattern string before matching.
Let's first look at how to represent different suffix substrings in the pattern string. Because the last character of the suffix substring is subscript M-1, we only need to record the length of the suffix substring, and a unique suffix substring can be determined by the length.
Substring representation
Then the key variable suffix array is introduced. The index of suffix array indicates the length of suffix substring. The array value corresponding to the subscript stores
Starting subscript value of good suffix matching in pattern string:
Suffix array definition
In this case, another matching start position of suffix substring C in the pattern string is 2, another matching start position of suffix substring BC in the pattern string is 1, another matching start position of suffix substring DBC in the pattern string is 0, and suffix substring cdbc only appears once in the pattern string, which is considered to be - 1.
Prefix array
It should be noted here that we should not only find another substring matching the good suffix in the pattern string, but also find the longest suffix substring matching the prefix substring of the pattern string in the suffix substring of the good suffix. For example:
Longest pattern matching
Suffix can only find another substring that matches a good suffix. However, a Boolean prefix array is also required to record whether the suffix substring of the pattern string can match the prefix substring of the pattern string.
Next, focus on how to fill the suffix and prefix arrays, take the substring with subscripts from 0 to I and the whole pattern string, and find the common suffix substring, where I = [0, m-2]. If the length of the common suffix substring is k, suffix [k] = J, where j represents the starting subscript of the common suffix substring. If J = 0, it means that the common suffix substring is also the prefix substring of the pattern string. At this time, prefix [k] = true.
Suffix and prefix arrays
//B = mode string, M = mode string length, suffix, prefix array, as defined above
private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
//Initialization
for (int i = 0; i 《 m; i++) {
suffix[i] = -1;
prefix[i] = false;
}
// b[0, i]
for (int i = 0; i 《 m - 1; i++) {
int j = i;
//Common suffix substring length
int k = 0;
//Find the common suffix substring with B [0, M-1], and there will be coverage.
while (j 》= 0 && b[j] == b[m-1-k]) {
--j;
++k;
//J + 1 represents the starting subscript of the common suffix substring in B [0, I]
suffix[k] = j+1;
}
//If the common suffix substring is also the prefix substring of the pattern string
if (j == -1) prefix[k] = true;
}
}
3.4.2 official code
With the suffix and prefix arrays, look at the move rules. Suppose the length of a good suffix string = k, if K= 0 indicates that there is a good suffix. Next, judge how to move by the value of suffix [k].
suffix[k] != - 1. When it is not equal to, it indicates that the pattern string is matched, and the pattern string is moved backward by j-suffix [k] + 1 bit, where j represents the character subscript in the pattern string corresponding to the bad character.
Suffix [k] = - 1. When it is equal to, it means that the good suffix does not match. It depends on the matching of the substring. The suffix substring length of the good suffix is B [R, M-1], where r = [J + 2, M-1], and the suffix substring length k = m-r. if prefix [k] = true, it means that the suffix substring with length k has a matching prefix substring, so we can move the pattern string backward by r bits.
If there is no match, move the pattern string back m bits directly.
//A and N represent the length of the main string and the main string respectively.
//B and m respectively represent the mode string and the mode string length.
public int bm(char[] a, int n, char[] b, int m) {
//Used to record the last position of each character in the mode string
in
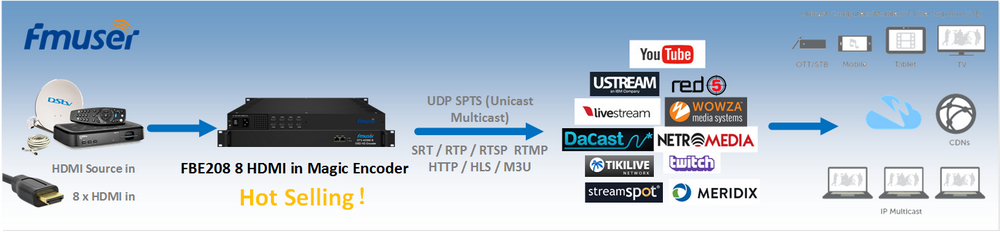
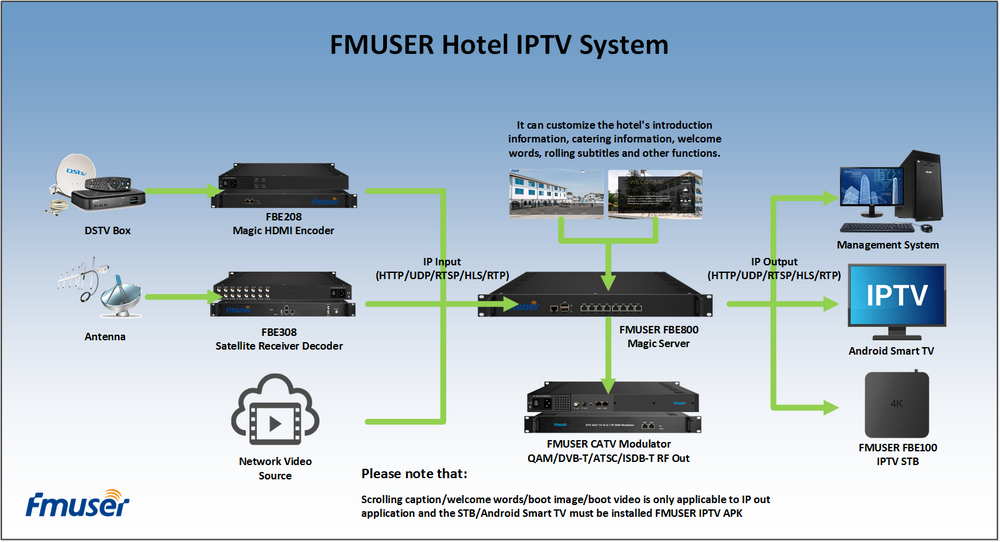
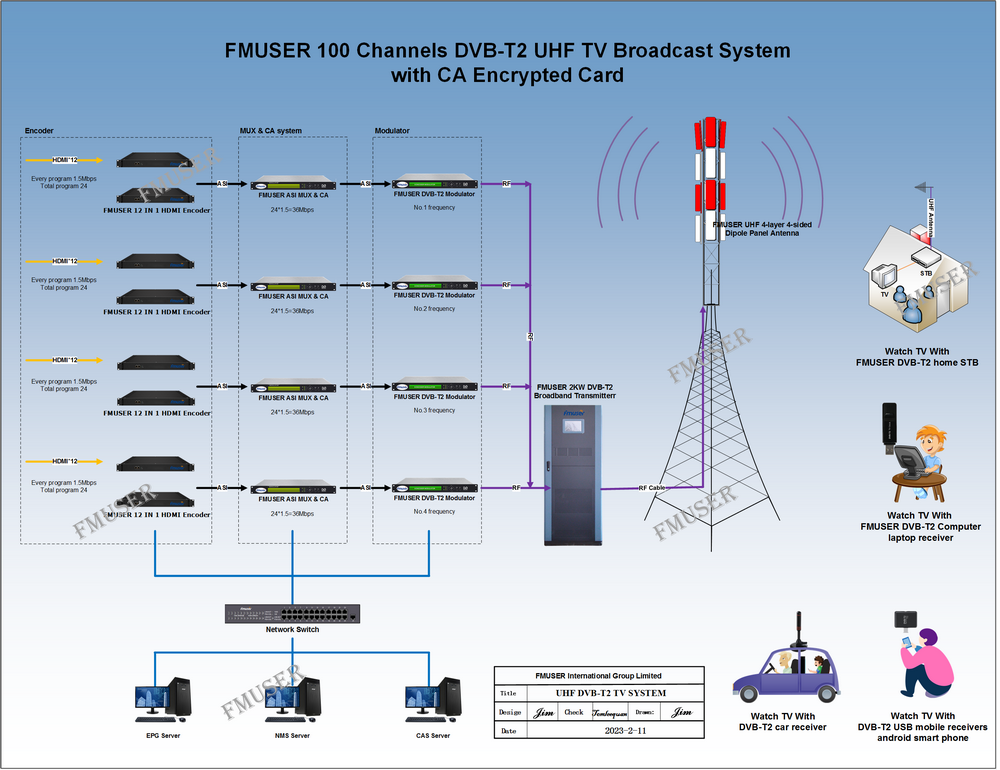
Our other product: