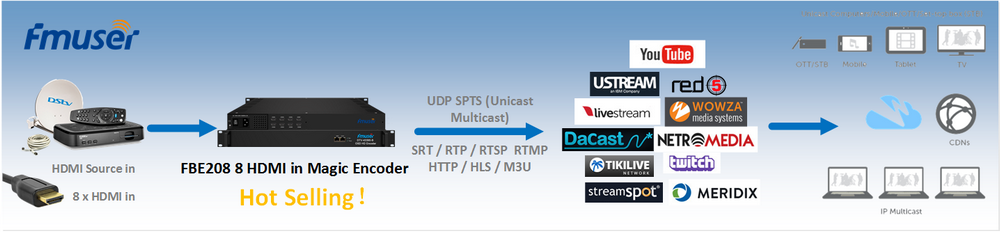
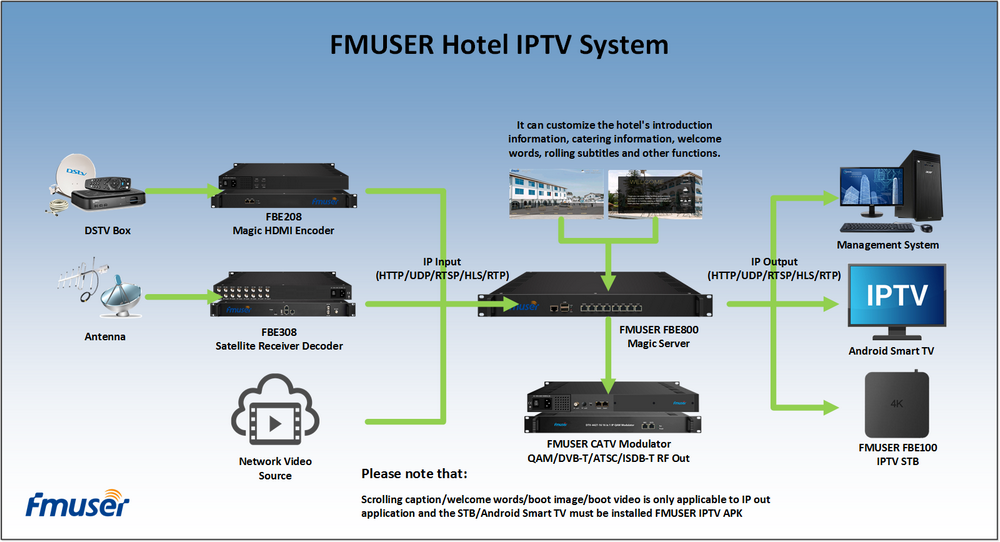
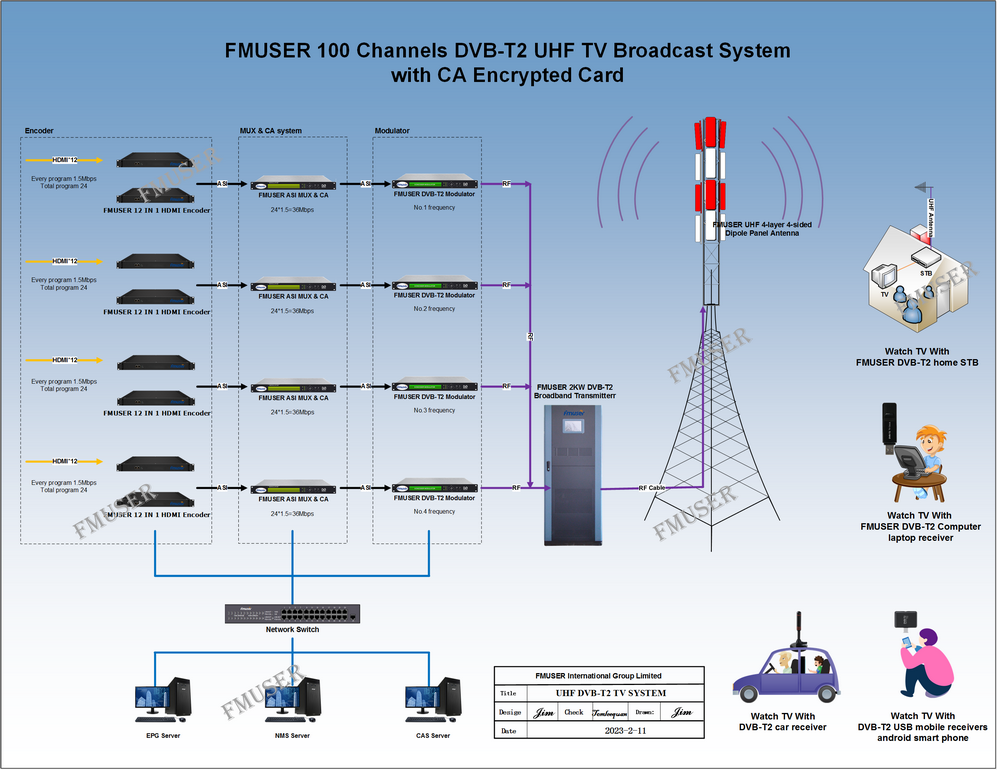
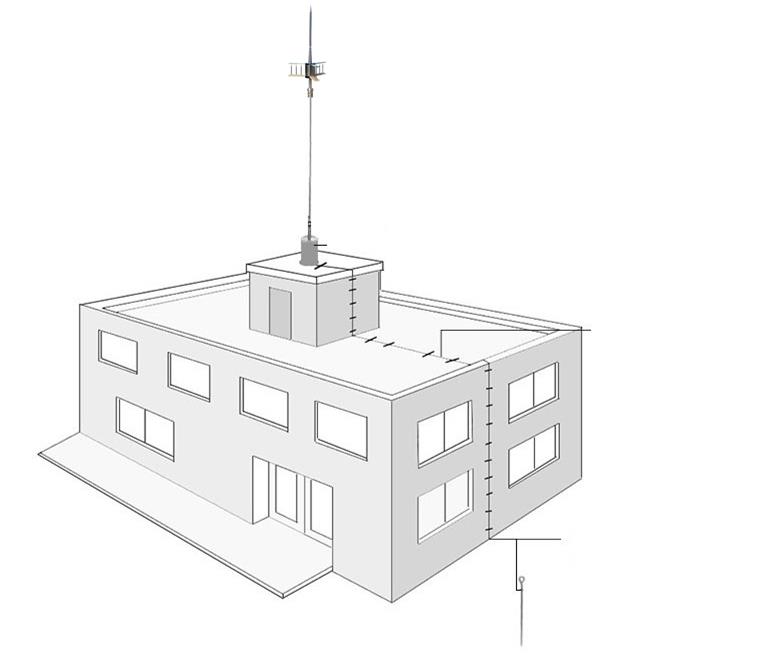
"H.264 / AVC Video Code Technology Detailed" video tutorial has been on "CSDN", which details the background, standard protocol and implementation of H.264, and through a practical engineering form to H.264 Standard analysis and implementation, welcome to watch!
"The paper is very shallow, perceived this matter", only the standard document is operated in the form of code, in order to have a sufficient understanding and understanding of the video compression coding standards!
Link address: H.264 / AVC video codec technology detailed
GitHub code address: Click here
1. Definition of the matrix
Matrix, English is called "Matrix", which is a very important concept in mathematics. From the form, the matrix can be represented by a table that consists of a number of M rows N columns. The following figure can represent a square matrix of 4 rows 4 columns:
In practical applications, matrices can play an important role in multiple technical fields such as audio and video compression coding, machine learning, artificial intelligence and other fields.
2. Battery operation
The matrix must be interacting with other data in the calculation. In the "linear algebra" we have clearly known that the matrix can be summed, multiplied, and multiplied by matrix. The matrix summary and the number of multiply are simple:
The matrix sum: the same type of matrix can be summed, so that the corresponding element is summarized and constitute a new matrix; the matrix number is multiplied: any matrix can be multiplied by the real number, and each element is multiplied by the number;
In contrast, the matrix will be slightly complicated with the matrix, and the necessary conditions are required, that is, the width of the matrix 1 must be equal to the taller of the matrix 2. The high and width of the product matrix is the high and matrix 2 of the matrix 1, respectively, as shown below:
Among them, the calculation method of the element of the product matrix is:
Typically, we will use only one or a matrix called vector. According to the aligned different, the vector and column vector are respectively referred to by line or column arrangement.
3. Linear transformation of vector and matrix
The linear transformation of the vector is defined as: Each element of the vector Y is a linear combination of elements in the vector x, then Y is the linear transformation of X. It is assumed that the vector [x1, x2, x3] and vector [Y1, Y2, Y3] are assumed, and the two vectors satisfy the following relationships:
Y1 = a11 * x1 + a12 * x2 + a13 * x3y2 = a21 * x1 + a22 * x2 + a23 * x3y3 = a31 * x1 + a32 * x2 + a33 * x3
Then we are called the vector [Y1, Y2, Y3] can be denoted by the vector [x1, x2, x3], and it is expressed as y = a · x in formula form. Its meaning can be expressed as a matrix multiplied by the vector:
The matrix A is a matrix of the linear transformation.
The transformation of the vector, the matrix can be considered constructed by the vector, so linear linear transform is equally applicable to the matrix transformation:
4. Vector orthogonality, orthogonal matrix and orthogonal transformation
To understand the orthogonality of the vector, you should first understand the concept of the vector of the vector. Under the "unstrue" condition, we can more understand the volume of the vector, that is, two identical length vectors corresponding to the sum of elements. Expressed with formulas:
The orthogon of the vector, equivalent to the volume of two vectors is 0. which is:
In the two-dimensional and three-dimensional space, the two orthogonal vectors are perpendicular to each other:
Since the matrix can be constructed of a plurality of column vectors, then a plurality of two orthogonal vents may constitute an orthogonal matrix. A matrix is the condition that the orthogonal matrix needs to meet:
The number of lines and the number of columns, that is, the orthogonal matrix is square; each column vector is unit vector, that is, the length is 1; each column is two or two orthogonal;
As mentioned earlier, each matrix can correspond to a linear transformation. Then, if a linear transform corresponds to the transformation matrix is an orthogonal matrix, then the transformation is an orthogonal change. One of the significant features of orthogonal transform is that the length of the vector does not change after orthogonal shift.
5. Discrete cosine transformation
Discrete Cosine Transform (DCT) is similar to a real type of discrete Fourier transform (DFT), which defines a variety of forms (refer to Wikipedia: Discrete cosine transformation). Discrete cosine transforms used in common applications are an orthogonal transform, and their positive transform and inverse transformation is calculated, such as:
Since the DCT has a characteristic similar to the DFT, the DCT can also realize the functions such as the information energy set. For image data, DCT can effectively concentrate most of the energy and low frequency portions, which also becomes one of the theoretical basis of transform coding in video compression. In fact, DCT has long-term applications with multiple images and video compression coding standards:
Video: MPEG-1 / MPEG-2; Image: JPEG
In H.264 and updated video compression standards, the Optimization of DCT is used to improve the version - integer transformation. The integer transformation effectively reduces the calculation complexity of the conversion operation to improve the operational efficiency of the codec.
Our other product: