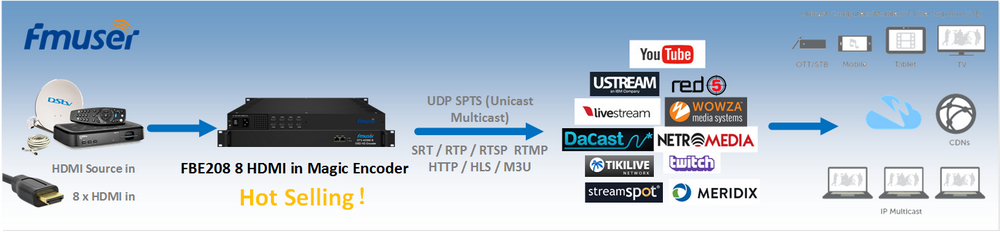
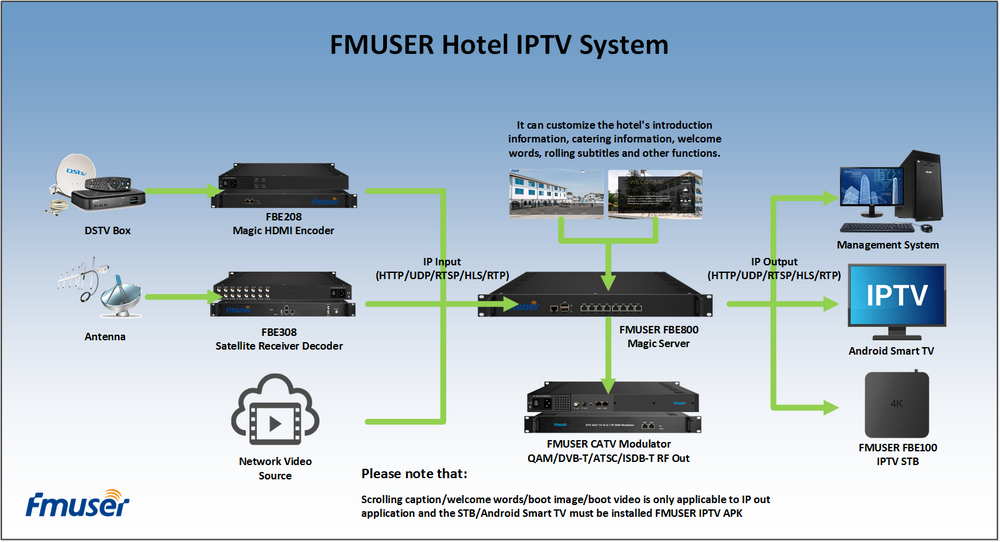
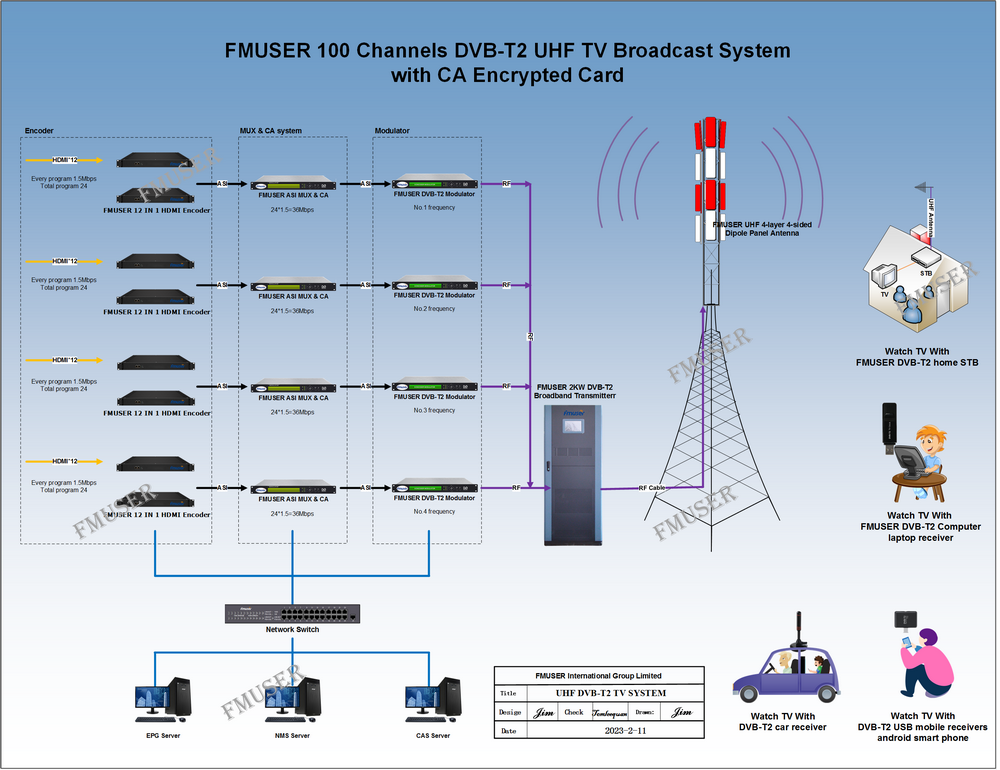
"In the first two notes, the author focused on the convolution principle in convolution neural network, deeply analyzed the principles of two-dimensional convolution and three-dimensional convolution, and fully understood the key concepts of CNN, such as convolution, pooling, full connection, filter, receptive field and so on. This section will continue to follow the previous DNN learning route. Before using tensorflow to build the neural network, try to manually build the convolution neural network using numpy, in order to have a deeper understanding of the convolution mechanism, forward propagation and back propagation principles and processes of the convolution neural network. One step convolution process before formally building CNN, we first define a one-step convolution process using numpy according to the understanding of linear calculation of convolution mechanism mentioned in the previous notes. The code is as follows: def conv_ single_ step(a_ slice_ prev, W, b):
s = a_ slice_ prev * W # Sum over all entries of the volume s.
Z = np.sum(s) # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
Z = float (Z + b) return Z in the above one-step convolution definition, we introduced an area to be convoluted input from the previous layer, namely receptive field a_ slice_ Prev, filter W, that is, the weight parameter and deviation B of the convolution layer. A one-step convolution process can be realized by performing linear calculation of Z = Wx + B. CNN forward propagation process: as in DNN, even if CNN has more convolution and pooling processes, the model is still a training process of forward propagation and back propagation. The forward propagation of CNN includes convolution and pooling. First, let's see how to use numpy to realize the complete convolution process based on the one-step convolution defined above. Convolution calculation is not difficult. We have realized it in one-step convolution. The difficulty lies in how to realize the scanning and moving process of the filter on the input image matrix. Among them, we need to find out some variables and parameters, as well as the shape of each input and output, which is very important for us to perform convolution and matrix multiplication. Firstly, our input is the original image matrix or the image output matrix of the previous layer after activation. Here, the activated output of the previous layer shall prevail. We must specify the shape of the input pixel, then the filter matrix and deviation, and also consider the step and filling, On this basis, we define the following forward convolution process based on filter movement and one-step convolution: def conv_ forward(A_ prev, W, b, hparameters): """"""
Arguments:
A_ prev -- output activations of the previous layer, numpy array of shape (m, n_ H_ prev, n_ W_ prev, n_ C_ prev)
W -- Weights, numpy array of shape (f, f, n_ C_ prev, n_ C)
b -- Biases, numpy array of shape (1, 1, 1, n_ C)
hparameters -- python dictionary containing ""stride"" and ""pad""
Returns:
Z -- conv output, numpy array of shape (m, n_ H, n_ W, n_ C)
cache -- cache of values needed for the conv_ backward() function
""""""
#Shape input from previous layer
(m, n_ H_ prev, n_ W_ prev, n_ C_ prev) = A_ Prev.shape # filter weighted shape
(f, f, n_ C_ prev, n_ C) = w.shape # stride parameter
Stripe = hpparameters ['stripe '] # fill parameters
Pad = hpparameters ['pad '] # calculate the height and width of the output image
n_ H = int((n_ H_ prev + 2 * pad - f) / stride + 1)
n_ W = int((n_ W_ Prev + 2 * pad - F) / Stripe + 1) # initialize output
Z = np.zeros((m, n_ H, n_ W, n_ C) ) # perform edge fill on input
A_ prev_ pad = zero_ pad(A_ prev, pad) for i in range(m):
a_ prev_ pad = A_ prev_ pad[i, :, :, :]
for h in range(n_ H):
for w in range(n_ W):
for c in range(n_ C):
#The filter scans the input image
vert_ start = h * stride
vert_ end = vert_ start + f
horiz_ start = w * stride
horiz_ end = horiz_ Start + F # define receptive field
a_ slice_ prev = a_ prev_ pad[vert_ start : vert_ end, horiz_ start : horiz_ End,:] # perform one-step convolution on the receptive field
Z[i, h, w, c] = conv_ single_ step(a_ slice_ prev, W[:,:,:,c], b[:,:,:,c]) assert(Z.shape == (m, n_ H, n_ W, n_ C))
cache = (A_ Prev, W, B, hpparameters) return Z, cache so that we have defined a complete convolution calculation process in the forward propagation of convolutional neural network. Generally speaking, we will add a relu activation operation to the output after convolution, as shown in Figure 2 above. We will omit it here. CNN forward propagation process: pooling is simply to take the maximum value of the local region. The forward propagation of pooling is similar to the convolution process, but it is relatively simple. There is no need to perform the product operation such as one-step convolution. Also note the parameters and input / output shapes. Therefore, we define the following forward propagation pooling process: def pool_ forward(A_ prev, hparameters, mode = ""max""): """"""
Arguments:
A_ prev -- Input data, numpy array of shape (m, n_ H_ prev, n_ W_ prev, n_ C_ prev)
hparameters -- python dictionary containing ""f"" and ""stride""
mode -- the pooling mode you would like to use, defined as a string (""max"" or ""average"")
Returns:
A -- output of the pool layer, a numpy array of shape (m, n_ H, n_ W, n_ C)
cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters
""""""
#Shape input from previous layer
(m, n_ H_ prev, n_ W_ prev, n_ C_ prev) = A_ Prev.shape # stride and weight parameters
f = hparameters[""f""]
Stripe = hpparameters ["" stripe ""] # calculates the height and width of the output image
n_ H = int(1 + (n_ H_ prev - f) / stride)
n_ W = int(1 + (n_ W_ prev - f) / stride)
n_ C = n_ C_ Prev # initialization output
A = np.zeros((m, n_ H, n_ W, n_ C))
for i in range(m):
for h in range(n_ H):
for w in range(n_ W):
for c in range (n_ C):
#The tree pool scans on the input image
vert_ start = h * stride
vert_ end = vert_ start + f
horiz_ start = w * stride
horiz_ end = horiz_ Start + F # defines the pooled area
a_ prev_ slice = A_ prev[i, vert_ start:vert_ end, horiz_ start:horiz_ End, c] # select the pool type
if mode == ""max"":
A[i, h, w, c] = np.max(a_ prev_ slice) elif mode == ""average"":
A[i, h, w, c] = np.mean(a_ prev_ slice)
cache = (A_ prev, hparameters) assert(A.shape == (m, n_ H, n_ W, n_ C) ) return a, cache it can be seen from the above code structure that the code structure of the forward propagation pooling process is very similar to the convolution process. CNN back propagation process: after convolution defines forward propagation, the difficulty and key point is how to define back propagation process for convolution and pooling process. The back propagation of convolution layer is always a complex process. As long as we define the forward propagation process in tensorflow, the back propagation will be calculated automatically. But using numpy to build CNN back propagation has to be defined by ourselves. The key is to accurately define the gradient of the loss function for each variable: from the above gradient calculation formula and the forward propagation process of convolution, we define the following convolution back propagation function: def conv_ backward(dZ, cache): """"""
Arguments:
dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_ H, n_ W, n_ C)
cache -- cache of values needed for the conv_ backward(), output of conv_ forward()
Returns:
dA_ prev -- gradient of the cost with respect to the input of the conv layer (A_ prev),
numpy array of shape (m, n_ H_ prev, n_ W_ prev, n_ C_ prev)
dW -- gradient of the cost with respect to the weights of the c
Our other product: