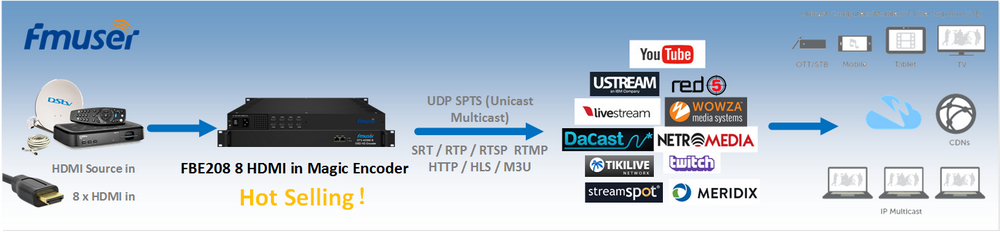
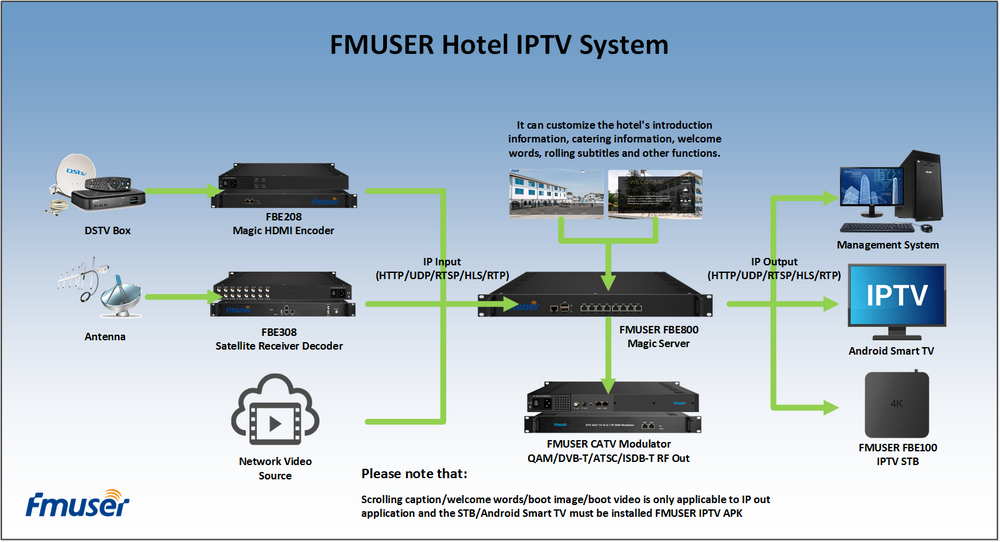
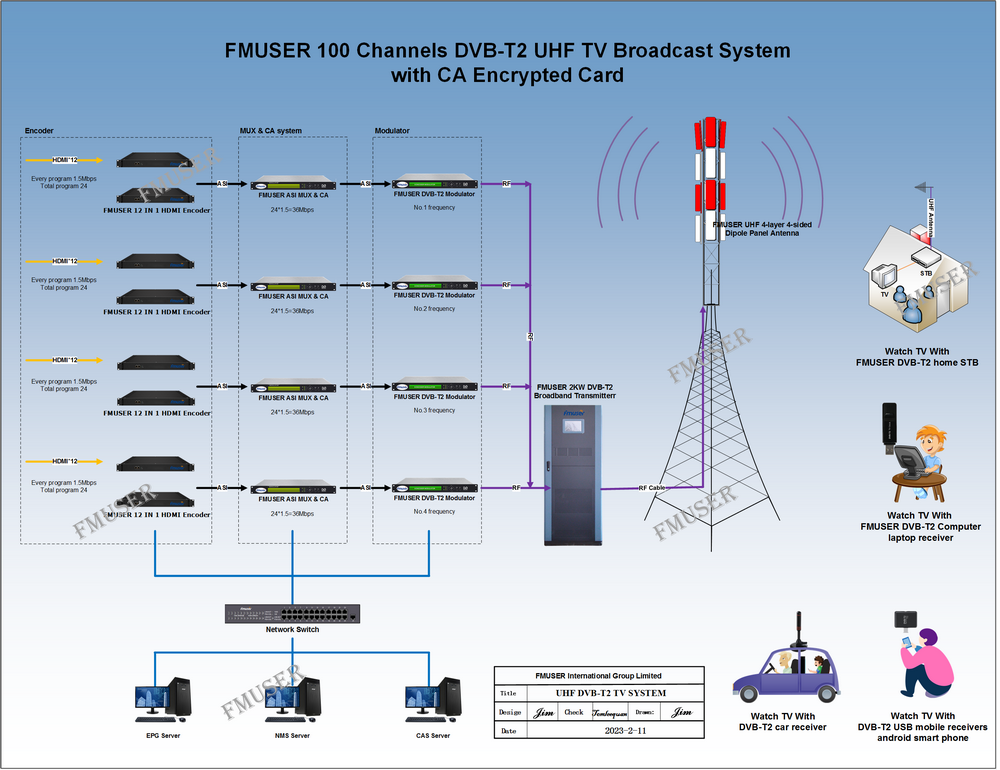
"This is a stag based framework we have just implemented. We named it graphchain. Then we will discuss design options and main challenges, and finally give conclusions.
If you are interested in its source, I first wrote this paper with Xavier boyen and Thomas Haines in 2016 - graphchain: an extensible decentralized ledger without blockchain. We put it on eprint, and there may be a more readable version on ERIM news. This paper has been published elsewhere, but these two places may be the easiest to find.
What is DAG?
First, what does DAG mean? It refers to a directed acyclic graph. This is a mathematical term in graph theory, which usually contains a set of vertices and edges. Edges are ordered pairs of vertices, which are usually represented by arrows in directed graphs. If you can't start from a vertex and return to a vertex along the arrow, the graph is acyclic. You may realize that this is not entirely a mathematical term.
The following figure is an example of DAG. Arrows represent edges and orange boxes represent vertices. You can check that there are no rings in the figure. You cannot start from one of the orange boxes and return to an orange box along the arrow. This is a DAG. You can also mark these DAGs.
If you do this, you will get a so-called poset. In our work, we talked a lot about posets. The idea here is that if you define that the arrow points to a vertex higher than the starting point to get a partial order, you will easily find that K is the highest of all the letters. You can also quickly find that for F and h, there is no order between them. All we know is that f and H are both higher than D and both lower than I.
Therefore, it is a partial order. Unlike another dag we are familiar with, that is, blockchain (below), it is completely ordered. In fact, if you start thinking about how to deal with these solitary blocks and how many solitary blocks there will be, you will find it really interesting. I don't have time to go into this topic, but it's really interesting, trust me. You will get bifurcation, but the blockchain is essentially DAG, but they are more restricted. You can't have all these extra partial orders.
Why do we need DAG?
What do we want to solve? The main problem we are trying to solve here is decentralization and scalability. Blockchain technology has many problems. These are probably the two most frequently talked about issues - there are some other issues, but the two issues I am most interested in are decentralization, which actually boils down to security issues and scalability issues, which are related to availability. Scalability issues remain. Where do these problems come from? These problems seem to stem from the use of transaction blocks? Maybe so.
The goal of our whole project is: can we create a system to pay off individual efforts? The main problem, as you may have realized, is that the ore pool has caused some problems. The reason for their problems is that they actually have a little too much power - some people think they have too much power. I tend to understand this. This is not necessarily a bad thing. There are many arguments for and against them. I really don't want to get involved in this topic, but wouldn't it be better if we didn't need them?
Can we eliminate the motivation to join the pool? This is one of the problems. In addition, whether this can also allow faster transaction processing. What if we could broadcast transactions with workload certificates attached, sort out these transactions and build a diagram with them? So, do we still need blocks? At least, this is based on the idea of DAG.
Why is this important? Because 51% of honest users are enough? no We already know that. So, what is decentralization? This is a more difficult problem. It's a little confused with the concept of distributed design, so you may ask what decentralization means. In fact, I think this question is difficult to answer. Many people think about the real meaning of centralization in the past, especially in cryptocurrency. In general, we want many independent machines running the same system all over the world. If so, all machines can be guaranteed to be computationally equivalent. Like I said, it's not new. People have been talking about it for a while.
What are we talking about? We're talking about pools and mines. On "independent machines running the same system all over the world" - in fact, the machine is running a pit system. And, from the point of view of computationally equivalent machines, we have mines. Therefore, in essence, we have a very powerful machine. The second issue I don't think is something DAG has to deal with. This depends on the function.
However, scalability is also a major problem. When we talk about blockchain, why should we care about scalability? Because blockchain is a linear set of blocks, one transaction refers to the next transaction. The problem is that no matter what type of blockchain is processed, blocks contain a certain number of transactions. Transactions can be received within a specific time period. As we have just heard, we know the limitations of Ethereum and bitcoin.
Part of the problem is that we have blocks and bind them with so many transactions, so we may have two different blocks, one containing transactions T1 to TN and the other containing transactions T1 to TN '. We don't know if they are the same - maybe they contain the same list of transactions, maybe not.
Using blockchain, if there is a split, we must choose one of them. It's a fork, isn't it. Therefore, we are now waiting to see which one will be expanded before we can determine which transactions we know. If I have some transactions in t ', now I will have to wait for them to be included somewhere later. We cannot rely on the transactions contained.
Of course, this is just the usual situation. Imagine that you have produced a large number of blocks at the same time due to some abnormal events. Using blockchain +, that is, the content of Ethereum and ghost protocols, you have uncle blocks that can be included. It's a very clever idea, but it won't include the deal. Therefore, you can still reward someone's efforts, which is a very wise idea about creating this additional block, because people should be rewarded for their efforts.
In essence, the whole idea is: can we also have a system in which you can create a new block containing transactions from T and t ', that is, the collection of these transactions?
This is essentially graphchain. What we have is: what would happen if there were no blocks? The transaction only refers to the previous transaction, any number can be used. To send a transaction, simply collect your approved transactions and quote them, and attach some proof of workload to the transaction.
How does this work?
We can define an abstract workload proof function. This is a rather abstract idea, but it is easy to implement through hash function in practice. Suppose that the workload proof function s contains problem a and its solution B. If B is the solution of a, we say s (a, b) is true. Taking the blockchain as an example, the solution may be a nonce. Your a refers to the transaction collection, links with previous blocks and all other data.
We want to quantify the workload so that we can say that the workload of this workload proof function = D. We can do this, most of the time. If you can partially reverse a hash function, you can say that it must cost so much computation, or we expect it to cost so much computation.
So we can do this, and this has happened, because the mine pool is essentially doing the same thing. If you work for a mine, instead of solving the block and giving it to them, you prove that you are working for them by showing them that you have solved a smaller problem. So, if you are in bitcoin, you may want to find a value below a certain threshold. You show them that you have found a solution below a higher threshold - but at least it shows that you are working for them.
In essence, we can use the same method. The purpose is to quantify the work done to solve a problem. Abstract function can be any difficulty that we can quantify to find the solution of the problem. We don't even need hash functions. You can imagine other ways to do this. Once again, we try to imagine it as a framework. We can broadcast transactions with related workload. The purpose of this is that we can say: here is a block with a workload of 8.
So you take the DAG again, and then you can imagine some numbers, and you can say: Well, now that we have all these numbers, what does that mean? Good question. What we need to do is to define the two concepts of weight and height. This is very similar to blockchain because you have accumulated workload. Once we have marked the graph with workload, we can mark it with other values.
For example, for weights, we relate this cumulative workload to transactions and all their descendants. Height is the cumulative workload associated with the transaction and all its ancestors. For example, you will find that weight is essentially adding the value of workload proof in each transaction.
Therefore, we can say (below), the weight of the transaction is 61. Why do you say that? Because it allows us to slowly establish the concept of the nesting degree of the transaction in the system. For height, you have a system that calculates all sub transactions. Interestingly, the transaction itself is also included. Therefore, for the second transaction (also in dark red in the figure below), we can say that its height is 80. In essence, these are only two examples, but what we want to say is that we can establish a concept that the height of a transaction in the graph is based on the proof of the workload it contains.
One more thing needs to be done in DAG based systems. We need to start removing further declining transactions. The reason why we have to do this is that if we give you a new chart, so you haven't seen any transactions recently, and you must immediately calculate how high they are, it will soon become very computationally expensive as the number of transactions in the system increases. You must limit this and eventually begin to get rid of further retreating transactions. This is a separate matter.
This DAG based design adds complexity, which is very tricky. In essence, we do this in order to obtain this convergence. If the transaction can reference any other previous transaction, what prevents users from creating new transactions on very old nodes?
You need to provide motivation. This is also part of the framework. We need incentives and want users to build new transactions from the top of the graph, so rewards are associated with some function of height. So, for the sake of simplicity, I've only written this. However, this is not so simple. For example, if this function is an inverse function, it will not work properly. But you do need some function of height to create this incentive to work from the front. The key to doing this is that we can execute the transaction and encourage people to start working at the front of the transaction. We didn't specify this because we were trying to develop a framework.
The key to convergence is that you end up with a green deal that is basically at the top of the list. It is a convergent transaction, and each transaction below it is part of its ancestor. Moreover, according to this function, everyone wants to build the new green transaction - if you want to build a new transaction, you will reference the top transaction. That's the idea.
However, we have other concerns. We have to worry about something like double flowers. Let's consider a double flower scenario. You have such a transaction chart (as shown below), and suddenly these two red transactions are spending a certain amount of money.
OK, how do you overcome this problem? Compare these transactions. Eventually you have to compare these and decide which one you want to continue to use. Imagine you have an active opponent. We can summarize the fragmentation in the system as: what happens if the opponent essentially wants to maintain the fragmentation of the system forever? Basically, you can generalize it into two graphs that can't be used as a basis, because you can't reference two conflicting transactions. Do they need double flowers and ensure that the system never converges?
The current situation for counterparties is that they must build on one of these two transactions. They must also catch up with other nodes in the network, which are trying to build on one of the transactions. Therefore, imagine a situation where an honest node, or more specifically, an incentive compatible node, first creates a transaction high enough, as if "this is a new real picture", and then the counterparty must create a new transaction on another chain. We can assign it some probabilities. Then this happens again and again, and so on, and you will eventually get such a probability (as follows).
You can see that it quickly becomes very small. But this is only effective when the opponent does not have more than half of the computing power. This is one of its arguments.
Just to give you an overview of graphchain: you create transactions at your own pace, and you will be rewarded for your personal efforts. Influenced by incentives, you prefer to create transactions at the top, and we allow multiple transactions to gain convergence. The proof of workload is built closer to real-time, so I hope you have these much smaller transactions created by individuals, and the proof of workload is established by the individuals of the transactions. Finally, the framework is agnostic to the workload proof function, or even to some extent to the reward function.
Differences with existing DAG systems
So you may have heard of other DAG systems. Iota is probably the most famous. For some time, its market value was very high. The main difference is that it does not actually have any incentives - there is a way of mining, but there are no incentives. They are currently using coordinators. But they are very similar in block diagram and content. The block diagram used by their website is very similar to the diagram I just showed. You can check it. It's actually very interesting.
Other implementations: byteball -- they look a bit similar, but differ in terms of trusted witnesses. Nano adopts distributed proof of interest protocol to eliminate conflicts through voting. Both systems are cool. I suggest you study them. They obviously have their own advantages and disadvantages. Our framework attempts to become more agnostic and decentralized.
conclusion
I am not only engaged in academic research - we have this paper - I also develop this framework full-time at NTNU in Norway and make it an effective cryptocurrency. I gave a speech on Norwegian national television about six months ago, and then I talked with these tto (technology transfer office) personnel. Now I'm trying to develop it into an effective cryptocurrency - for fun, it's really difficult. But we are still in the initial stage of the project. We recently
Our other product: